unbonded electrons in 3d drawing

Spin states when describing transition metal coordination complexes refers to the potential spin configurations of the central metal's d electrons. In many these spin states vary between high-spin and low-spin configurations. These configurations tin can be understood through the ii major models used to describe coordination complexes; crystal field theory and ligand field theory, which is a more advanced version based on molecular orbital theory.^[i]

High-spin vs. low-spin [edit]

Octahedral complexes [edit]

Low-spin [Iron(NO_ii)_vi]³⁻ crystal field diagram

The Δ splitting of the d orbitals plays an important office in the electron spin state of a coordination complex. 3 factors bear on Δ: the menses (row in periodic table) of the metallic ion, the charge of the metal ion, and the field strength of the circuitous'southward ligands every bit described past the spectrochemical series. Only octahedral complexes of first row transition metals prefer high-spin states.

In order for low spin splitting to occur, the energy price of placing an electron into an already singly occupied orbital must be less than the toll of placing the additional electron into an e _k orbital at an free energy cost of Δ. If the energy required to pair 2 electrons is greater than the energy cost of placing an electron in an e _g , Δ, loftier spin splitting occurs.

If the separation betwixt the orbitals is large, then the lower free energy orbitals are completely filled earlier population of the college orbitals according to the Aufbau principle. Complexes such as this are called "depression-spin" since filling an orbital matches electrons and reduces the full electron spin. If the separation betwixt the orbitals is small enough then it is easier to put electrons into the college energy orbitals than it is to put two into the same depression-energy orbital, considering of the repulsion resulting from matching two electrons in the same orbital. So, one electron is put into each of the five d orbitals earlier whatever pairing occurs in accord with Hund's dominion resulting in what is known every bit a "loftier-spin" circuitous. Complexes such as this are chosen "high-spin" since populating the upper orbital avoids matches between electrons with opposite spin.

Loftier-spin [FeBr_six]³⁻ crystal field diagram

The charge of the metal center plays a role in the ligand field and the Δ splitting. The higher the oxidation state of the metal, the stronger the ligand field that is created. In the result that at that place are two metals with the same d electron configuration, the ane with the college oxidation land is more likely to be low spin than the one with the lower oxidation state. For example, Feⁱⁱ⁺ and Co³⁺ are both d⁶; however, the higher charge of Co^three+ creates a stronger ligand field than Iron²⁺. All other things being equal, Fe²⁺ is more than likely to be high spin than Co^three+.

Ligands likewise affect the magnitude of Δ splitting of the d orbitals according to their field strength as described by the spectrochemical series. Strong-field ligands, such equally CN⁻ and CO, increase the Δ splitting and are more likely to be low-spin. Weak-field ligands, such as I⁻ and Br⁻ cause a smaller Δ splitting and are more likely to exist high-spin.

Some octahedral complexes exhibit spin crossover, where the loftier and low spin states exist is dynamic equilibrium.

Light-induced spin-crossover of [Fe(pyCH_twoNH₂)₃]²⁺, which switches from high and low-spin.^[two]

Tetrahedral complexes [edit]

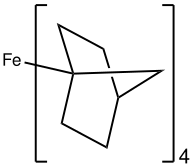
Atomic number 26(4-norbornyl)₄ is a rare example of a low-spin tetrahedral complex.

The Δ splitting energy for tetrahedral metallic complexes (four ligands), Δ_tet is smaller than that for an octahedral complex. Consequently, tetrahedral complexes are almost always loftier spin^[3] Examples of low spin tetrahedral complexes include Atomic number 26(2-norbornyl)₄,^[iv] [Co(4-norbornyl)₄]⁺, and the nitrosyl complex Cr(NO)((N(tms)₂)₃.

Square planar complexes [edit]

Many d⁸ complexes of the start row metals exist in tetrahedral or square planar geometry. In some cases these geometries exist in measurable equilibria. For example, dichlorobis(triphenylphosphine)nickel(II) has been crystallized in both tetrahedral and square planar geometries.^[v]

Ligand field theory vs crystal field theory [edit]

In terms of d-orbial splitting, ligand field theory (LFT) and crystal field theory (CFT) give similar results. CFT is an older, simpler model that treats ligands every bit point charges. LFT is more than chemic, emphasizes covalent bonding and accommodates pi-bonding explicitly.

High-spin and depression-spin systems [edit]

In the case of octahedral complexes, the question of loftier spin vs low spin start arises for d^iv, since it has more than the 3 electrons to make full the not-bonding d orbitals according to ligand field theory or the stabilized d orbitals co-ordinate to crystal field splitting.

All complexes of second and third row metals are depression-spin.

d^four

Octahedral high-spin: 4 unpaired electrons, paramagnetic, substitutionally labile. Includes Cr²⁺. Many complexes assigned every bit Cr(II) are however Cr(III) with reduced ligands.^[vi]), Mn³⁺.

Octahedral low-spin: 2 unpaired electrons, paramagnetic, substitutionally inert. Includes Cr²⁺, Mn³⁺.

d^five

Octahedral high-spin: 5 unpaired electrons, paramagnetic, substitutionally labile. Includes Fe³⁺, Mn²⁺. Example: Tris(acetylacetonato)iron(Three).

Octahedral depression-spin: 1 unpaired electron, paramagnetic, substitutionally inert. Includes Iron³⁺. Example: [Fe(CN)₆]³⁻.

d⁶

Octahedral loftier-spin: 4 unpaired electrons, paramagnetic, substitutionally labile. Includes Fe^two+, Coⁱⁱⁱ⁺. Examples: [Fe(H_iiO)₆]ⁱⁱ⁺, [CoF_six]³⁻.

Octahedral low-spin: no unpaired electrons, diamagnetic, substitutionally inert. Includes Fe²⁺, Ni⁴⁺. Example: [Co(NH₃)_six]³⁺.

d⁷

Octahedral high-spin: 3 unpaired electrons, paramagnetic, substitutionally labile. Includes Co²⁺, Ni³⁺.

Octahedral low-spin:ane unpaired electron, paramagnetic, substitutionally labile. Includes Co²⁺, Ni^three+. Example: [Co(NH_three)_vi]ⁱⁱ⁺.

d⁸

Octahedral loftier-spin: ii unpaired electrons, paramagnetic, substitutionally labile. Includes Ni²⁺. Example: [Ni(NH₃)_{half dozen}]ⁱⁱ⁺.

Tetrahedral high-spin: two unpaired electrons, paramagnetic, substitutionally labile. Includes Niⁱⁱ⁺. Instance: [NiCl₄]^2-.

Square planar low-spin: no unpaired electrons, diamagnetic, substitutionally inert. Includes Ni²⁺. Example: [Ni(CN)_iv]²⁻.

Ionic radii [edit]

The spin state of the circuitous affects an atom's ionic radius. For a given d-electron count, high-spin complexes are larger.^[vii]

d⁴

Octahedral high spin: Cr^two+, 64.v pm.

Octahedral low spin: Mn³⁺, 58 pm.

d^five

Octahedral loftier spin: Fe³⁺, the ionic radius is 64.5 pm.

Octahedral low spin: Iron³⁺, the ionic radius is 55 pm.

d⁶

Octahedral high spin: Fe²⁺, the ionic radius is 78 pm, Co^three+ ionic radius 61 pm.

Octahedral low spin: Includes Feⁱⁱ⁺ ionic radius 62 pm, Co^three+ ionic radius 54.5 pm, Ni^iv+ ionic radius 48 pm.

d⁷

Octahedral high spin: Coⁱⁱ⁺ ionic radius 74.5 pm, Ni^three+ ionic radius 60 pm.

Octahedral low spin: Co²⁺ ionic radius 65 pm, Ni³⁺ionic radius 56 pm.

d⁸

Octahedral high spin: Niⁱⁱ⁺ ionic radius 69 pm.

Square planar low-spin: Ni²⁺ ionic radius 49 pm.

Ligand substitution rates [edit]

By and large, the rates of ligand dissociation from depression spin complexes are lower than dissociation rates from high spin complexes. In the instance of octahedral complexes, electrons in the eastward_{one thousand} levels are anti-bonding with respect to the metal-ligand bonds. Famous "substitution inert" complexes are octahedral complexes of d³ and low-spin d^vi metal ions, illustrated respectfully past Cr³⁺ and Co³⁺.^[8]

References [edit]

1. ^ Miessler, Gary 50.; Donald A. Tarr (1998). Inorganic Chemistry (second edition). Upper Saddle River, New Jersey: Pearson Education, Inc. Pearson Prentice Hall. ISBN0-thirteen-841891-8.
2. ^ Gütlich, P. (2001). "Photoswitchable Coordination Compounds". Coordination Chemistry Reviews. 219–221: 839–879. doi:10.1016/S0010-8545(01)00381-ii.
3. ^ Zumdahl, Steven (2009). "19.half-dozen Transition Metals and Coordination Chemical science: The Crystal Field Model". Chemical Principles. Cengage Learning, Inc. ISBN978-0538734561.
4. ^ Bower, Barton K.; Tennent, Howard G. (1972). "Transition metal Bicyclo[ii.2.1]hept-1-yls". Journal of the American Chemic Society. 94 (seven): 2512–2514. doi:10.1021/ja00762a056.
5. ^ Batsanov, Andrei Due south.; Howard, Judith A. K. (2001). "trans-Dichlorobis(triphenylphosphine)nickel(2) Bis(dichloromethane) Solvate: Redetermination at 120 Thou". Acta Crystallogr E. 57: 308–309. doi:10.1107/S1600536801008741.
6. ^ Scarborough, Christopher C.; Sproules, Stephen; Doonan, Christian J.; Hagen, Karl Southward.; Weyhermüller, Thomas; Wieghardt, Karl (2012). "Scrutinizing Low-Spin Cr(2) Complexes". Inorganic Chemistry. 51 (12): 6969–6982. doi:x.1021/ic300882r. PMID 22676275.
7. ^ Shannon R.D. (1976). "Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides". Acta Crystallographica. A32: 751-767. doi:ten.1107/S0567739476001551.
8. ^ R. G. Wilkins (1991). Kinetics and Mechanism of Reactions of Transition metal Complexes, 2d Thoroughly Revised Edition. Weinheim: VCH. doi:ten.1002/bbpc.19920960429. ISBN3-527-28389-7.

silvapulds1984.blogspot.com

Source: https://en.wikipedia.org/wiki/Spin_states_(d_electrons)

Share this post